A “linear” system must exhibit both homogeneity and superposition. Linear systems are interesting because they are easier to analyze than non-linear systems.

Superposition holds true if: \( f(x_1+x_2)=f(x_1) + f(x_2) \)

Homogeneity holds true if: \( f(Kx)=Kf(x) \)

Ohm’s law is normally written as v = iR. But you could also write it where voltage is a function of current. e.g. f(i) = iR.

\( f(i_1+i+2) = f(i_1) + f(i_2) \)

Superposition applies to Ohm’s law. It doesn’t matter whether you add currents and then compute voltage, or compute both voltages and add them.

Also, doubling current doubles voltage (2 is your constant), so homogeneity applies too.

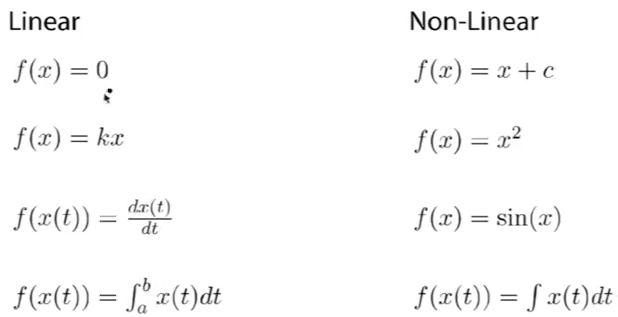
Linearity Examples

Using Superposition to Understand Linear Circuits

  • Zero-out all independent sources (i.e. short your voltage sources and open your current sources).
  • Return each source, one at a time, and solve for values of interest.
  • Sum the values of your results.