Formulae, constants, laws, etc.

  • Coulomb = C
    • Electrons per coulomb: \( 6.241509745 * 10^{18} \)
    • Coulombs per electron: \( 1.602 x 10^{-19} \)
  • Coulomb’s Law:
\[ \left F \right = k_{e}\frac{q_{1}q_{2}}{r^{2}} \]
  • … where
    • \( k_{e} \) is a constant
    • \( q_{1} \) is the charge of the first particle in Coulombs
    • \( q_{2} \) is the charge of the second particle in Coulombs
    • r is the distance between them in meters
    • F is the force in newtons
    • m is meters
    • N is Newtons
    • \( k_{e}=8.988 \ast 10^{9} \frac{Nm^2}{C^2} \)
  • Meter: Abbreviated m.
  • Centimeter: Abbreviated cm.
  • Newton: Unit of force. Force needed to accelerate 1 kilogram of mass at the rate of 1 meter per second squared. Abbreviated N.
  • Amp: Unit of current. Abbreviated A.
    • Amps = Coulombs / seconds
    • \( A=\frac{C}{s}\)
  • Joule: Unit of work (or energy expended). Abbreviated J. Newtons * meters.
    • 1 Joule = passing an electric current of one amp through a resistance of one ohm for one second
    • Other measures of work/energy expended:
      • Watts * seconds
      • Coulombs * volts
  • Volts are joules divided by coulombs. i.e. 1V = \( \frac{1J}{1C} \)
  • Watts:
    • Joules per second
    • Volts * Amps
  • Current arrows
    Forward (positive):

    Forward current

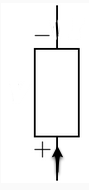
From plus, through to minus is forward (consuming power).

Reverse (negative):

Reverse current

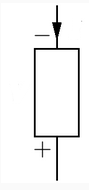
From minus, through to plus is backward (generating power).

For voltages, + connected to + is forward.

Another way of diagramming the same thing

Forward/reverse currents

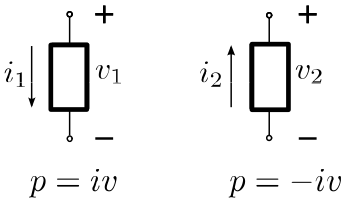
  • Ohm’s Law:
    • v = iR
      • If current arrow is from minus, through to plus, then use v = -iR
    • \( \Omega=\frac{V}{A} \)
      • Volts / Amps
  • Metric prefixes
    • k = kilo = \( 10^{3} \)
    • M = mega = \( 10^{6} \)
    • c = centi = \( 10^{-2} \)
    • m = milli = \( 10^{-3} \)
    • \( \mu \) = micro = \( 10^{-6} \)
  • Kirchhoff’s Current Law: The sum of all currents entering a node = the sum of all currents leaving a node.
  • Resistors in series: \( R_{1} + R_{2} + R_{3} \)

  • Resistors in parallel: \( \left ( \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} \right )^{-1} \) or use \( \frac{R_1 R_2}{R_1 + R_2} \)

  • Voltage divider (using resistors in series): \( v_1=\frac{R_1}{R_1+R_2}v \)

  • Current divider (using resistors in parallel): \( i_1=\frac{R_2}{R_1+R_2}i \)

  • Capacitance in Farads: \[ C = \frac{Q}{V} \]
    • C = Farads
    • Q = Coulombs
    • V = Volts
  • 1 microfarad = 1 \( \mu \)F \( = 1 \times 10^{-6} \) farad
  • 1 picofarad = 1 pF = \( 1 \times 10^{-12} \) farad = 1 micro microfarad